- Details
- Kategorie: Hilfsmittel

Kürzlich habe ich auf Instagram meine selbst erstellte Übersicht über die Stampin' Blends gezeigt. Ausgedruckt auf dem Papier, auf dem man die Alkoholmarker auch nutzen möchte (in diesem Fall Flüsterweiß), sieht man direkt, wie die unterschiedlichen Farbtöne und die jeweils helle und dunkle Version einer Farbe wirken. Gerne stelle ich dir meine beiden Dateien als PDF zur Verfügung:
Die Übersicht "Saisonkatalog" ist bei weitem noch nicht voll, sodass noch Platz für künftig erscheinende oder nicht mehr erhältliche Farben ist. Die Informationen dazu kannst du ganz einfach handschriftlich ergänzen.
Ich hoffe, das Ganze ist dir ebenfalls eine gute Hilfe. Über dein Feedback würde ich mich sehr freuen.
- Details
- Kategorie: Hilfsmittel

Bei meinen Workshops stelle ich immer wieder fest, dass natürlich nicht jedem all diese "Fremdwörter" aus der Bastelszene ein Begriff sind - mir ging es da anfangs nicht anders. Was sind noch gleich Dimensionals (oder heißen die Dinger doch "Demolitions")? Und was ist ein Brad, wenn nicht gerade ein berühmter Schauspieler? Daher dachte ich mir, dass ich hier die Begriffe in alphabetischer Reihenfolge mit einer kurzen Erklärung aufliste, wobei die Liste im Laufe der Zeit sicherlich noch ergänzt wird. Um direkt zu einem bestimmten Buchstaben zu gelangen, kannst du diesen einfach anklicken.
- Details
- Kategorie: Hilfsmittel
Im Mai habe ich anhand eines Produktvorstellungs-Videos und zahlreicher Tippkiste-Videos den tollen Stamparatus von Stampin' Up! vorgestellt. An dieser Stelle findest du eine Übersicht mit all den wunderbaren Techniken, die mit diesem Tool möglich sind. Die jeweiligen Video-Tutorials werden nach Anklicken der Vorschau-Grafik geladen.
Hinge Step Stamping

Ich bin dazu verpflichtet, dich darauf hinzuweisen, dass durch Betrachten dieses Videos standardmäßig Daten an YouTube übermittelt werden. Nähere Informationen findst du in der Datenschutzerklärung.
Stanzen-Template

Ich bin dazu verpflichtet, dich darauf hinzuweisen, dass durch Betrachten dieses Videos standardmäßig Daten an YouTube übermittelt werden. Nähere Informationen findst du in der Datenschutzerklärung.
Farbig embossen

Ich bin dazu verpflichtet, dich darauf hinzuweisen, dass durch Betrachten dieses Videos standardmäßig Daten an YouTube übermittelt werden. Nähere Informationen findst du in der Datenschutzerklärung.
Schatten stempeln

Ich bin dazu verpflichtet, dich darauf hinzuweisen, dass durch Betrachten dieses Videos standardmäßig Daten an YouTube übermittelt werden. Nähere Informationen findst du in der Datenschutzerklärung.
Ombré-Look

Ich bin dazu verpflichtet, dich darauf hinzuweisen, dass durch Betrachten dieses Videos standardmäßig Daten an YouTube übermittelt werden. Nähere Informationen findst du in der Datenschutzerklärung.
Kaleidoskop-stempeln

Ich bin dazu verpflichtet, dich darauf hinzuweisen, dass durch Betrachten dieses Videos standardmäßig Daten an YouTube übermittelt werden. Nähere Informationen findst du in der Datenschutzerklärung.
Stempelmotive spiegeln

Ich bin dazu verpflichtet, dich darauf hinzuweisen, dass durch Betrachten dieses Videos standardmäßig Daten an YouTube übermittelt werden. Nähere Informationen findst du in der Datenschutzerklärung.
Klatsch-Technik

Ich bin dazu verpflichtet, dich darauf hinzuweisen, dass durch Betrachten dieses Videos standardmäßig Daten an YouTube übermittelt werden. Nähere Informationen findst du in der Datenschutzerklärung.
- Details
- Kategorie: Hilfsmittel
Ich liebe das Envelope Punchboard (EPB), es hat mir aber auch schon reichlich Kopfzerbrechen beschert, als ich eine passende Schachtel für einen Smarties-Adventskalender entwerfen wollte. Und Unmengen Altpapier, das beim Testen, Anpassen, wieder Testen usw. entstanden ist. Ich hatte zwar nachher meine passende Schachtel, doch es geht auch einfacher - und deutlich Zeit- und Ressourcen sparender. Wie das? Mit der ultimativen Formel kannst du Umschläge und Schachteln in jeder beliebigen Größe entwerfen (lediglich die Größe des Papiers schränkt dich ein). Am Ende dieses mathematischen Beitrags findest du eine Excel-Tabelle zum kostenlosen Herunterladen, mit der du im Handumdrehen die passenden Papiermaße und Stanzungen ermitteln kannst.
Die ultimative Formel für Umschläge
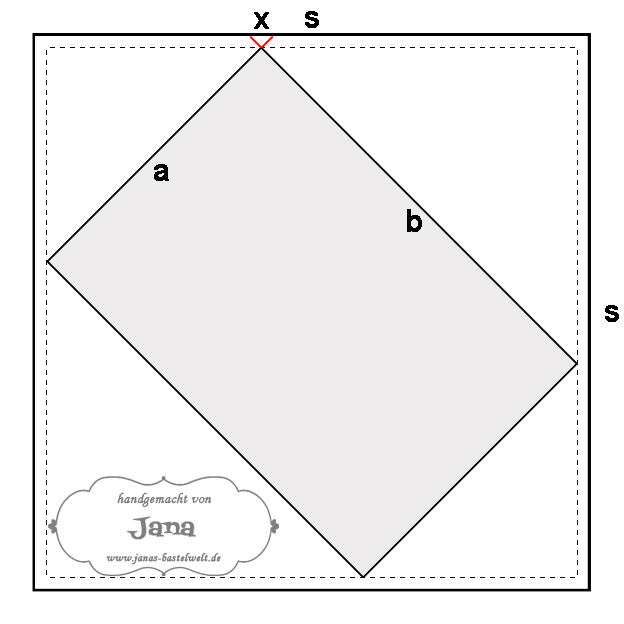
Ein kleiner Ausflug in die längst vergangene Schulzeit: Zunächst musst du wissen, wie groß die Karte ist und dann noch wenige Millimeter hinzugeben, damit sie auch leicht in den Umschlag gleitet und nicht hakt. Die kurze Seite nennen wir a, die lange b und das Papierquadrat, das wir im folgenden berechnen, hat die Seitenlänge s. Und bedenke immer: Punktrechnung vor Strichrechnung und die Berechnung in den Klammern wird zuerst vorgenommen ;)
Berechnen wir also die Seitenlänge des quadratischen Papiers, das die Grundlage für unseren Umschlag bildet. Dies geht mit dieser Formel:
s = (a + b) ÷ √2 + 2 cm
Als nächstes müssen wir wissen, wo wir das erste Mal stanzen und falzen. Das lässt sich mit dieser Formel berechnen:
x = a ÷ √2 + 1 cm
Damit du dir das Ganze bildlich vor Augen führen kannst, hier eine entsprechende Grafik:
Beispielrechnung gefällig? Nehmen wir an, wir möchten einen Umschlag mit den Maßen 10 x 15 cm anfertigen. Dann beträgt die Seitenlänge des quadratischen Papiers
s= (10 + 15) ÷ √2 + 2 cm = 19,7 cm (gerundet)
Nun müssen wir noch ausrechnen, an welcher Stelle wir das erste Mal stanzen und falzen:
x = 10 ÷ √2 + 1 cm = 8,1 cm (gerundet)
Gar nicht so schwer, oder?
Die ultimative Formel für Schachteln
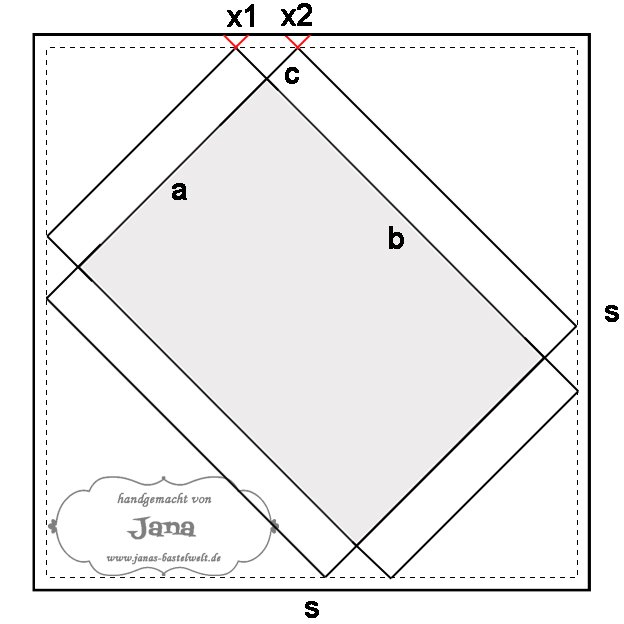
Auch hierbei gilt: Die kurze Seite nennen wir a, die lange b und die Seitenlänge des quadratischen Papiers s. Hinzu kommt nun noch die Höhe der Schachtel mit Namen c. Zudem sind bei einer Schachtel zwei Stanzungen und Falzrillen nötig.
Die Seitenlänge s des quadratischen Papiers berechnet sich wie folgt:
s = (a + b + 2 × c) ÷ √2 + 2 cm
Die 1. Stanzung und Falzung (x1) erfolgt nach dieser Formel:
x1 = a ÷ √2 + 1 cm
Und die 2. Stanzung und Falzung (x2) berechnet man wie folgt:
x2 = (a + 2 × c) ÷ √2 + 1 cm
Zur Veranschaulichung habe ich wieder eine Grafik vorbereitet:
Um das Ganze besser nachvollziehbar zu machen, berechnen wir hier einfach mal eine Beispiel-Schachtel mit den Maßen 10 x 15 x 2 cm.
Die Seitenlänge des quadratischen Papiers beträgt in diesem Fall:
s = (10 + 15 + 4) ÷ √2 + 2 cm = 22,5 cm (gerundet)
Die erste Stanzung und Falzung erfolgt bei:
x1 = 10 ÷ √2 + 1 cm = 8,1 cm (gerundet)
Die zweite Stanzung und Falzung berechnet sich wie folgt:
x2 = (10 + 4) ÷ √2 + 1 cm = 10,9 cm (gerundet)
Mit Hilfe eines Taschenrechners ebenfalls fix errechnet und einer wunderbaren Schachtel steht nichts mehr im Wege.
Bedenke bitte, dass es kleine Rundungsdifferenzen gibt - insbesondere bei der Berechnung mit Inch, da das EPB lediglich in 1/8 Schritte eingeteilt ist.
Für alle, die bei Wurzelberechnungen Zahnweh bekommen, habe ich eine Excel-Tabelle angefertigt, in die ihr nur noch die gewünschten Maße in die grünen Felder eintragen braucht: Klick. Um diese nutzen zu können, einfach auf den PC herunterladen.